In [1]:
from dsc80_utils import *

Lecture 5 – Exploratory Data Analysis and Data Cleaning¶

DSC 80, Spring 2025¶

Agenda 📆¶

  • Dataset overview.
  • Introduction to plotly.
  • Exploratory data analysis and feature types.
  • Data cleaning.
    • Data quality checks.
    • Missing values.
    • Transformations and timestamps.
    • Modifying structure.
  • Investigating student-submitted questions!

Dataset overview¶

San Diego food safety¶

From this article (archive link):

In the last three years, one third of San Diego County restaurants have had at least one major food safety violation.

99% Of San Diego Restaurants Earn ‘A' Grades, Bringing Usefulness of System Into Question¶

From this article (archive link):

Food held at unsafe temperatures. Employees not washing their hands. Dirty countertops. Vermin in the kitchen. An expired restaurant permit.

Restaurant inspectors for San Diego County found these violations during a routine health inspection of a diner in La Mesa in November 2016. Despite the violations, the restaurant was awarded a score of 90 out of 100, the lowest possible score to achieve an ‘A’ grade.

The data¶

  • We downloaded the data about the 1000 restaurants closest to UCSD from here.
  • We had to download the data as JSON files, then process it into DataFrames. You'll learn how to do this soon!
    • Until now, you've (largely) been presented with CSV files that pd.read_csv could load without any issues.
    • But there are many different formats and possible issues when loading data in from files.
    • See Chapter 8 of Learning DS for more.
In [2]:
rest_path = Path('data') / 'restaurants.csv'
insp_path = Path('data') / 'inspections.csv'
viol_path = Path('data') / 'violations.csv'
In [3]:
rest = pd.read_csv(rest_path)
insp = pd.read_csv(insp_path)
viol = pd.read_csv(viol_path)

Question 🤔 (Answer at dsc80.com/q)

Code: lec05-dfs

The first article said that one third of restaurants had at least one major safety violation.
Which DataFrames and columns seem most useful to verify this?

In [5]:
rest.head(2)
Out[5]:
business_id name business_type address ... lat long opened_date distance
0 211898487641 MOBIL MART LA JOLLA VILLAGE Pre-Packaged Retail Market 3233 LA JOLLA VILLAGE DR, LA JOLLA, CA 92037 ... 32.87 -117.23 2002-05-05 0.62
1 211930769329 CAFE 477 Low Risk Food Facility 8950 VILLA LA JOLLA DR, SUITE# B123, LA JOLLA,... ... 32.87 -117.24 2023-07-24 0.64

2 rows × 12 columns

In [6]:
rest.columns
Out[6]:
Index(['business_id', 'name', 'business_type', 'address', 'city', 'zip',
       'phone', 'status', 'lat', 'long', 'opened_date', 'distance'],
      dtype='object')
In [7]:
insp.head(2)
Out[7]:
custom_id business_id inspection_id description ... completed_date status link status_link
0 DEH2002-FFPN-310012 211898487641 6886133 NaN ... 2023-02-16 Complete http://www.sandiegocounty.gov/deh/fhd/ffis/ins... http://www.sandiegocounty.gov/deh/fhd/ffis/ins...
1 DEH2002-FFPN-310012 211898487641 6631228 NaN ... 2022-01-03 Complete http://www.sandiegocounty.gov/deh/fhd/ffis/ins... http://www.sandiegocounty.gov/deh/fhd/ffis/ins...

2 rows × 11 columns

In [8]:
insp.columns
Out[8]:
Index(['custom_id', 'business_id', 'inspection_id', 'description', 'type',
       'score', 'grade', 'completed_date', 'status', 'link', 'status_link'],
      dtype='object')
In [9]:
viol.head(2)
Out[9]:
inspection_id violation major_violation status violation_text correction_type_link violation_accela link
0 6886133 Hot and Cold Water Y Out of Compliance - Major Hot and Cold Water http://www.sandiegocounty.gov/deh/fhd/ffis/vio... 21. Hot & cold water available http://www.sandiegocounty.gov/deh/fhd/ffis/vio...
1 6631228 Hot and Cold Water N Out of Compliance - Minor Hot and Cold Water http://www.sandiegocounty.gov/deh/fhd/ffis/vio... 21. Hot & cold water available http://www.sandiegocounty.gov/deh/fhd/ffis/vio...
In [10]:
viol.columns
Out[10]:
Index(['inspection_id', 'violation', 'major_violation', 'status',
       'violation_text', 'correction_type_link', 'violation_accela', 'link'],
      dtype='object')

Introduction to plotly¶

plotly¶

  • We've used plotly in lecture briefly, and you even have to use it in Project 1 Question 13, but we haven't yet discussed it formally.
  • It's a visualization library that enables interactive visualizations.
No description has been provided for this image

Using plotly¶

There are a few ways we can use plotly:

  • Using the plotly.express syntax.
    • plotly is very flexible, but it can be verbose; plotly.express allows us to make plots quickly.
    • See the documentation here – it's very rich (there are good examples for almost everything).
  • By setting pandas plotting backend to 'plotly' (by default, it's 'matplotlib') and using the DataFrame plot method.
    • The DataFrame plot method is how you created plots in DSC 10!

For now, we'll use plotly.express syntax; we've imported it in the dsc80_utils.py file that we import at the top of each lecture notebook.

Initial plots¶

First, let's look at the distribution of inspection 'score's:

In [16]:
#insp['score']
fig = px.histogram(insp['score'])
fig

How about the distribution of average inspection 'score' per 'grade'?

In [19]:
scores = (
    insp[['grade', 'score']]
    .dropna()
    .groupby('grade')
    .mean()
    .reset_index()
)
#scores
# x= and y= are columns of scores. Convenient!
px.bar(scores, x='grade', y='score')
In [20]:
# Same as the above!
scores.plot(kind='bar', x='grade', y='score')

Exploratory data analysis and feature types¶

The data science lifecycle, revisited¶

No description has been provided for this image

We're at the stage of understanding the data.

Exploratory data analysis (EDA)¶

  • Historically, data analysis was dominated by formal statistics, including tools like confidence intervals, hypothesis tests, and statistical modeling.

  • In 1977, John Tukey defined the term exploratory data analysis, which described a philosophy for proceeding about data analysis:

Exploratory data analysis is actively incisive, rather than passively descriptive, with real emphasis on the discovery of the unexpected.

  • Practically, EDA involves, among other things, computing summary statistics and drawing plots to understand the nature of the data at hand.

The greatest gains from data come from surprises… The unexpected is best brought to our attention by pictures.

Different feature types¶

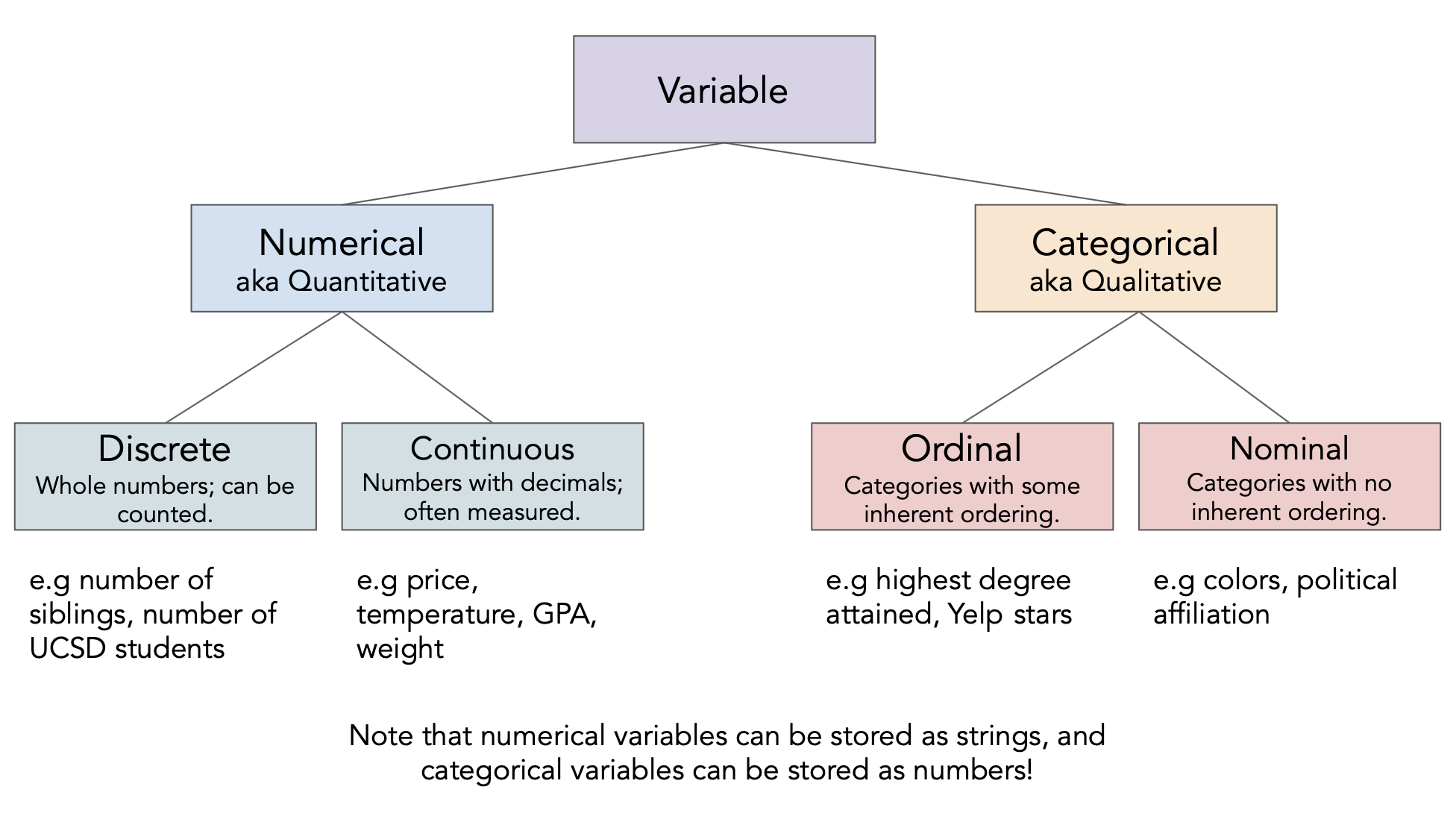
No description has been provided for this image

Question 🤔 (Answer at dsc80.com/q)

Code: lec05-types

Determine the feature type of each of the following variables.

  • insp['score']
  • insp['grade']
  • viol['violation_accela']
  • viol['major_violation']
  • rest['business_id']
  • rest['opened_date']
In [45]:
...
Out[45]:
Ellipsis

Feature types vs. data types¶

  • The data type pandas uses is not the same as the "data type" we talked about just now!

    • There's a difference between feature type and computational data type.

  • Take care when the two don't match up very well!

In [46]:
# pandas stores these as ints, but they're actually nominal.
rest['business_id']
Out[46]:
0      211898487641
1      211930769329
2      211909057778
           ...     
997    211899338714
998    211942150255
999    211925713322
Name: business_id, Length: 1000, dtype: int64
In [47]:
# pandas stores these as strings, but they're actually numeric.
rest['opened_date']
Out[47]:
0      2002-05-05
1      2023-07-24
2      2019-01-22
          ...    
997    2002-05-05
998    2016-11-03
999    2022-11-03
Name: opened_date, Length: 1000, dtype: object

Data cleaning¶

Four pillars of data cleaning¶

When loading in a dataset, to clean the data – that is, to prepare it for further analysis – we will:

  1. Perform data quality checks.

  2. Identify and handle missing values.

  3. Perform transformations, including converting time series data to timestamps.

  4. Modify structure as necessary.

Data cleaning: Data quality checks¶

Data quality checks¶

We often start an analysis by checking the quality of the data.

  • Scope: Do the data match your understanding of the population?
  • Measurements and values: Are the values reasonable?
  • Relationships: Are related features in agreement?
  • Analysis: Which features might be useful in a future analysis?

Scope¶

Do the data match your understanding of the population?

We were told that we're only looking at the 1000 restaurants closest to UCSD, so the restaurants in rest should agree with that.

In [49]:
rest.sample(5)
Out[49]:
business_id name business_type address ... lat long opened_date distance
869 211912304517 SWEET MAHINA Class B Cottage Food Operation 4551 MT LA PLATTA PL, SAN DIEGO, CA 92117-3045 ... 32.83 -117.19 2021-08-31 4.47
935 211906499771 THE GOLF BAR Restaurant Food Facility 5583 CLAIREMONT MESA BLVD, SAN DIEGO, CA 92117 ... 32.83 -117.17 2019-10-11 4.84
187 211984552427 LEMONADE Restaurant Food Facility 4545 LA JOLLA VILLAGE DR, SUITE# D-35, SAN DIE... ... 32.87 -117.21 2014-12-12 1.51
902 211944527313 DAVANTI ENOTECA Restaurant Food Facility 12955 EL CAMINO REAL, SUITE# G-3, SAN DIEGO, C... ... 32.95 -117.24 2020-02-24 4.68
640 211903875703 MAGDA'S BAKERY Class A Cottage Food Operation 6505 MUIRLANDS DR, LA JOLLA, CA 92037-6350 ... 32.83 -117.26 2020-09-16 3.76

5 rows × 12 columns

Measurements and values¶

Are the values reasonable?

Do the values in the 'grade' column match what we'd expect grades to look like?

In [50]:
insp['grade'].value_counts()
Out[50]:
grade
A    2978
B      11
Name: count, dtype: int64

What kinds of information does the insp DataFrame hold?

In [51]:
insp.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 5179 entries, 0 to 5178
Data columns (total 11 columns):
 #   Column          Non-Null Count  Dtype  
---  ------          --------------  -----  
 0   custom_id       5179 non-null   object 
 1   business_id     5179 non-null   int64  
 2   inspection_id   5179 non-null   int64  
 3   description     0 non-null      float64
 4   type            5179 non-null   object 
 5   score           5179 non-null   int64  
 6   grade           2989 non-null   object 
 7   completed_date  5179 non-null   object 
 8   status          5179 non-null   object 
 9   link            5179 non-null   object 
 10  status_link     5179 non-null   object 
dtypes: float64(1), int64(3), object(7)
memory usage: 445.2+ KB

What's going on in the 'address' column of rest?

In [22]:
# Are there multiple restaurants with the same address?
rest['address'].value_counts()
Out[22]:
address
5300 GRAND DEL MAR CT, SAN DIEGO, CA 92130       9
8657 VILLA LA JOLLA DR, LA JOLLA, CA 92037       8
4545 LA JOLLA VILLAGE DR, SAN DIEGO, CA 92122    8
                                                ..
3963 GOVERNOR DR, SAN DIEGO, CA 92122            1
4041 GOVERNOR DR, SAN DIEGO, CA 92122-2520       1
2672 DEL MAR HEIGHTS RD, DEL MAR, CA 92014       1
Name: count, Length: 863, dtype: int64
In [23]:
# Keeps all rows with duplicate addresses.
(
    rest
    .groupby('address')
    .filter(lambda df: df.shape[0] >= 2)
    .sort_values('address')
)
Out[23]:
business_id name business_type address ... lat long opened_date distance
406 211899308875 NASEEMS BAKERY & KABOB Restaurant Food Facility 10066 PACIFIC HEIGHTS BLVD, SAN DIEGO, CA 92121 ... 32.90 -117.19 2012-04-17 2.77
402 211898699154 HANAYA SUSHI CAFE Restaurant Food Facility 10066 PACIFIC HEIGHTS BLVD, SAN DIEGO, CA 92121 ... 32.90 -117.19 2011-03-22 2.77
401 211899558107 ARMANDOS MEXICAN FOOD Restaurant Food Facility 10066 PACIFIC HEIGHTS BLVD, SAN DIEGO, CA 92121 ... 32.90 -117.19 2005-06-28 2.77
... ... ... ... ... ... ... ... ... ...
575 211972411855 TARA HEATHER CAKE DESIGN Caterer 9932 MESA RIM RD, SUITE# A, SAN DIEGO, CA 9212... ... 32.90 -117.18 2014-04-24 3.51
344 211990537315 COMPASS GROUP FEDEX EXPRESS OLSON Pre-Packaged Retail Market 9999 OLSON DR, SAN DIEGO, CA 92121-2837 ... 32.89 -117.20 2022-10-19 2.27
343 211976587262 CANTEEN - FED EX OLSON Pre-Packaged Retail Market 9999 OLSON DR, SAN DIEGO, CA 92121-2837 ... 32.89 -117.20 2020-07-31 2.27

213 rows × 12 columns

In [24]:
# Does the same thing as above!
(
    rest[rest.duplicated(subset=['address'], keep=False)]
    .sort_values('address')
)
Out[24]:
business_id name business_type address ... lat long opened_date distance
406 211899308875 NASEEMS BAKERY & KABOB Restaurant Food Facility 10066 PACIFIC HEIGHTS BLVD, SAN DIEGO, CA 92121 ... 32.90 -117.19 2012-04-17 2.77
402 211898699154 HANAYA SUSHI CAFE Restaurant Food Facility 10066 PACIFIC HEIGHTS BLVD, SAN DIEGO, CA 92121 ... 32.90 -117.19 2011-03-22 2.77
401 211899558107 ARMANDOS MEXICAN FOOD Restaurant Food Facility 10066 PACIFIC HEIGHTS BLVD, SAN DIEGO, CA 92121 ... 32.90 -117.19 2005-06-28 2.77
... ... ... ... ... ... ... ... ... ...
575 211972411855 TARA HEATHER CAKE DESIGN Caterer 9932 MESA RIM RD, SUITE# A, SAN DIEGO, CA 9212... ... 32.90 -117.18 2014-04-24 3.51
344 211990537315 COMPASS GROUP FEDEX EXPRESS OLSON Pre-Packaged Retail Market 9999 OLSON DR, SAN DIEGO, CA 92121-2837 ... 32.89 -117.20 2022-10-19 2.27
343 211976587262 CANTEEN - FED EX OLSON Pre-Packaged Retail Market 9999 OLSON DR, SAN DIEGO, CA 92121-2837 ... 32.89 -117.20 2020-07-31 2.27

213 rows × 12 columns

Relationships¶

Are related features in agreement?

Do the 'address'es and 'zip' codes in rest match?

In [52]:
rest[['address', 'zip']]
Out[52]:
address zip
0 3233 LA JOLLA VILLAGE DR, LA JOLLA, CA 92037 92037
1 8950 VILLA LA JOLLA DR, SUITE# B123, LA JOLLA,... 92037-1704
2 6902 LA JOLLA BLVD, LA JOLLA, CA 92037 92037
... ... ...
997 1234 TOURMALINE ST, SAN DIEGO, CA 92109-1856 92109-1856
998 12925 EL CAMINO REAL, SUITE# AA4, SAN DIEGO, C... 92130
999 2672 DEL MAR HEIGHTS RD, DEL MAR, CA 92014 92014

1000 rows × 2 columns

What about the 'score's and 'grade's in insp?

In [53]:
insp[['score', 'grade']]
Out[53]:
score grade
0 96 NaN
1 98 NaN
2 98 NaN
... ... ...
5176 0 NaN
5177 0 NaN
5178 90 A

5179 rows × 2 columns

Analysis¶

Which features might be useful in a future analysis?

  • We're most interested in:

    • These columns in the rest DataFrame: 'business_id', 'name', 'address', 'zip', and 'opened_date'.
    • These columns in the insp DataFrame: 'business_id', 'inspection_id', 'score', 'grade', 'completed_date', and 'status'.
    • These columns in the viol DataFrame: 'inspection_id', 'violation', 'major_violation', 'violation_text', and 'violation_accela'.

  • Also, let's rename a few columns to make them easier to work with.

💡 Pro-Tip: Using pipe¶

When we manipulate DataFrames, it's best to define individual functions for each step, then use the pipe method to chain them all together.

The pipe DataFrame method takes in a function, which itself takes in a DataFrame and returns a DataFrame.

  • In practice, we would add functions one by one to the top of a notebook, then pipe them all.
  • For today, will keep re-running pipe to show data cleaning process.
In [54]:
def subset_rest(rest):
    return rest[['business_id', 'name', 'address', 'zip', 'opened_date']]

rest = (
    pd.read_csv(rest_path)
    .pipe(subset_rest)
)
rest
Out[54]:
business_id name address zip opened_date
0 211898487641 MOBIL MART LA JOLLA VILLAGE 3233 LA JOLLA VILLAGE DR, LA JOLLA, CA 92037 92037 2002-05-05
1 211930769329 CAFE 477 8950 VILLA LA JOLLA DR, SUITE# B123, LA JOLLA,... 92037-1704 2023-07-24
2 211909057778 VALLEY FARM MARKET 6902 LA JOLLA BLVD, LA JOLLA, CA 92037 92037 2019-01-22
... ... ... ... ... ...
997 211899338714 PACIFIC BEACH ELEMENTARY 1234 TOURMALINE ST, SAN DIEGO, CA 92109-1856 92109-1856 2002-05-05
998 211942150255 POKEWAN DEL MAR 12925 EL CAMINO REAL, SUITE# AA4, SAN DIEGO, C... 92130 2016-11-03
999 211925713322 SAFFRONO LOUNGE RESTAURANT 2672 DEL MAR HEIGHTS RD, DEL MAR, CA 92014 92014 2022-11-03

1000 rows × 5 columns

In [55]:
# Same as the above – but the above makes it easier to chain more .pipe calls afterwards.
subset_rest(pd.read_csv(rest_path))
Out[55]:
business_id name address zip opened_date
0 211898487641 MOBIL MART LA JOLLA VILLAGE 3233 LA JOLLA VILLAGE DR, LA JOLLA, CA 92037 92037 2002-05-05
1 211930769329 CAFE 477 8950 VILLA LA JOLLA DR, SUITE# B123, LA JOLLA,... 92037-1704 2023-07-24
2 211909057778 VALLEY FARM MARKET 6902 LA JOLLA BLVD, LA JOLLA, CA 92037 92037 2019-01-22
... ... ... ... ... ...
997 211899338714 PACIFIC BEACH ELEMENTARY 1234 TOURMALINE ST, SAN DIEGO, CA 92109-1856 92109-1856 2002-05-05
998 211942150255 POKEWAN DEL MAR 12925 EL CAMINO REAL, SUITE# AA4, SAN DIEGO, C... 92130 2016-11-03
999 211925713322 SAFFRONO LOUNGE RESTAURANT 2672 DEL MAR HEIGHTS RD, DEL MAR, CA 92014 92014 2022-11-03

1000 rows × 5 columns

Let's use pipe to keep (and rename) the subset of the columns we care about in the other two DataFrames as well.

In [56]:
def subset_insp(insp):
    return (
        insp[['business_id', 'inspection_id', 'score', 'grade', 'completed_date', 'status']]
        .rename(columns={'completed_date': 'date'})
    )

insp = (
    pd.read_csv(insp_path)
    .pipe(subset_insp)
)
In [57]:
def subset_viol(viol):
    return (
        viol[['inspection_id', 'violation', 'major_violation', 'violation_accela']]
        .rename(columns={'violation': 'kind',
                         'major_violation': 'is_major',
                         'violation_accela': 'violation'})
    )

viol = (
    pd.read_csv(viol_path)
    .pipe(subset_viol)
)

Combining the restaurant data¶

Let's join all three DataFrames together so that we have all the data in a single DataFrame.

In [58]:
def merge_all_restaurant_data():
    return (
        rest
        .merge(insp, on='business_id', how='left')
        .merge(viol, on='inspection_id', how='left')
    )

df = merge_all_restaurant_data()
df
Out[58]:
business_id name address zip ... status kind is_major violation
0 211898487641 MOBIL MART LA JOLLA VILLAGE 3233 LA JOLLA VILLAGE DR, LA JOLLA, CA 92037 92037 ... Complete Hot and Cold Water Y 21. Hot & cold water available
1 211898487641 MOBIL MART LA JOLLA VILLAGE 3233 LA JOLLA VILLAGE DR, LA JOLLA, CA 92037 92037 ... Complete Hot and Cold Water N 21. Hot & cold water available
2 211898487641 MOBIL MART LA JOLLA VILLAGE 3233 LA JOLLA VILLAGE DR, LA JOLLA, CA 92037 92037 ... Complete Holding Temperatures N 7. Proper hot & cold holding temperatures
... ... ... ... ... ... ... ... ... ...
8728 211925713322 SAFFRONO LOUNGE RESTAURANT 2672 DEL MAR HEIGHTS RD, DEL MAR, CA 92014 92014 ... Complete Equipment and Utensil Storage, Use N 35. Equipment / Utensils -approved, installed,...
8729 211925713322 SAFFRONO LOUNGE RESTAURANT 2672 DEL MAR HEIGHTS RD, DEL MAR, CA 92014 92014 ... Complete Toilet Facilities N 43. Toilet facilities -properly constructed, s...
8730 211925713322 SAFFRONO LOUNGE RESTAURANT 2672 DEL MAR HEIGHTS RD, DEL MAR, CA 92014 92014 ... Complete Floors, Walls, and Ceilings N 45. Floor, walls and ceilings - built, maintai...

8731 rows × 13 columns

Question 🤔 (Answer at dsc80.com/q)

Code: lec05-lefts

Why should the function above use two left joins? What would go wrong if we used other kinds of joins?

Data cleaning: Missing values¶

Missing values¶

Next, it's important to check for and handle missing values, as they can have a big effect on your analysis.

In [59]:
insp[['score', 'grade']]
Out[59]:
score grade
0 96 NaN
1 98 NaN
2 98 NaN
... ... ...
5176 0 NaN
5177 0 NaN
5178 90 A

5179 rows × 2 columns

In [60]:
# The proportion of values in each column that are missing.
insp.isna().mean()
Out[60]:
business_id      0.00
inspection_id    0.00
score            0.00
grade            0.42
date             0.00
status           0.00
dtype: float64
In [61]:
# Why are there null values here?
# insp['inspection_id'] and viol['inspection_id'] don't have any null values...
df[df['inspection_id'].isna()]
Out[61]:
business_id name address zip ... status kind is_major violation
759 211941133403 TASTY CHAI 8878 REGENTS RD 105, SAN DIEGO, CA 92122-5853 92122-5853 ... NaN NaN NaN NaN
1498 211915545446 EMBASSY SUITES SAN DIEGO LA JOLLA 4550 LA JOLLA VILLAGE DR, SAN DIEGO, CA 92122-... 92122-1248 ... NaN NaN NaN NaN
1672 211937443689 SERVICENOW 4770 EASTGATE MALL, SAN DIEGO, CA 92121-1970 92121-1970 ... NaN NaN NaN NaN
... ... ... ... ... ... ... ... ... ...
8094 211997340975 COOKIE SCOOP 7759 GASTON DR, SAN DIEGO, CA 92126-3036 92126-3036 ... NaN NaN NaN NaN
8450 211900595220 I LOVE BANANA BREAD CO 4068 DALLES AVE, SAN DIEGO, CA 92117-5518 92117-5518 ... NaN NaN NaN NaN
8545 211963768842 PETRA KITCHEN 5252 BALBOA ARMS DR 175, SAN DIEGO, CA 92117-4949 92117-4949 ... NaN NaN NaN NaN

29 rows × 13 columns

There are many ways of handling missing values, which we'll cover in an entire lecture next week. But a good first step is to check how many there are!

Data cleaning: Transformations and timestamps¶

Transformations and timestamps¶

From last class:

A transformation results from performing some operation on every element in a sequence, e.g. a Series.

It's often useful to look at ways of transforming your data to make it easier to work with.

  • Type conversions (e.g. changing the string "$2.99" to the number 2.99).

  • Unit conversion (e.g. feet to meters).

  • Extraction (Getting 'vermin' out of 'Vermin Violation Recorded on 10/10/2023').

Creating timestamps¶

Most commonly, we'll parse dates into pd.Timestamp objects.

In [63]:
# Look at the dtype!
insp['date']
Out[63]:
0       2023-02-16
1       2022-01-03
2       2020-12-03
           ...    
5176    2023-03-06
5177    2022-12-09
5178    2022-11-30
Name: date, Length: 5179, dtype: object
In [64]:
# This magical string tells Python what format the date is in.
# For more info: https://docs.python.org/3/library/datetime.html#strftime-and-strptime-behavior
date_format = '%Y-%m-%d'
pd.to_datetime(insp['date'])
Out[64]:
0      2023-02-16
1      2022-01-03
2      2020-12-03
          ...    
5176   2023-03-06
5177   2022-12-09
5178   2022-11-30
Name: date, Length: 5179, dtype: datetime64[ns]
In [65]:
# Another advantage of defining functions is that we can reuse this function
# for the 'opened_date' column in `rest` if we wanted to.
def parse_dates(insp, col):
    date_format = '%Y-%m-%d'
    dates = pd.to_datetime(insp[col], format=date_format)
    return insp.assign(**{col: dates})

insp = (
    pd.read_csv(insp_path)
    .pipe(subset_insp)
    .pipe(parse_dates, 'date')
)

# We should also remake df, since it depends on insp.
# Note that the new insp is used to create df!
df = merge_all_restaurant_data()
In [66]:
# Look at the dtype now!
df['date']
Out[66]:
0      2023-02-16
1      2022-01-03
2      2020-12-03
          ...    
8728   2022-11-30
8729   2022-11-30
8730   2022-11-30
Name: date, Length: 8731, dtype: datetime64[ns]

Working with timestamps¶

  • We often want to adjust granularity of timestamps to see overall trends, or seasonality.
  • Use the resample method in pandas (documentation).
    • Think of it like a version of groupby, but for timestamps.
    • For instance, insp.resample('2W', on='date') separates every two weeks of data into a different group.
In [67]:
insp.resample('2W', on='date')['score'].mean()
Out[67]:
date
2020-01-05    42.67
2020-01-19    59.33
2020-02-02    56.34
              ...  
2023-09-24    66.60
2023-10-08    59.58
2023-10-22    66.81
Freq: 2W-SUN, Name: score, Length: 100, dtype: float64
In [68]:
# Where are those numbers coming from?
insp[
    (insp['date'] >= '2020-01-05') &
    (insp['date'] < '2020-01-19')
]['score']
Out[68]:
10        0
11       92
12        0
       ... 
4709      0
4988    100
5107     96
Name: score, Length: 86, dtype: int64
In [70]:
(insp.resample('2W', on='date')
 .size()
 .plot(title='Number of Inspections Over Time')
)

The .dt accessor¶

Like with Series of strings, pandas has a .dt accessor for properties of timestamps (documentation).

In [71]:
insp['date']
Out[71]:
0      2023-02-16
1      2022-01-03
2      2020-12-03
          ...    
5176   2023-03-06
5177   2022-12-09
5178   2022-11-30
Name: date, Length: 5179, dtype: datetime64[ns]
In [72]:
insp['date'].dt.day
Out[72]:
0       16
1        3
2        3
        ..
5176     6
5177     9
5178    30
Name: date, Length: 5179, dtype: int32
In [73]:
insp['date'].dt.dayofweek
Out[73]:
0       3
1       0
2       3
       ..
5176    0
5177    4
5178    2
Name: date, Length: 5179, dtype: int32
In [75]:
dow_counts = insp['date'].dt.dayofweek.value_counts()
fig = px.bar(dow_counts)
fig.update_xaxes(tickvals=np.arange(7), ticktext=['Mon', 'Tues', 'Wed', 'Thurs', 'Fri', 'Sat', 'Sun'])

Data cleaning: Modifying structure¶

Reshaping DataFrames¶

We often reshape the DataFrame's structure to make it more convenient for analysis. For example, we can:

  • Simplify structure by removing columns or taking a set of rows for a particular period of time or geographic area.

    • We already did this!

  • Adjust granularity by aggregating rows together.

    • To do this, use groupby (or resample, if working with timestamps).

  • Reshape structure, most commonly by using the DataFrame melt method to un-pivot a dataframe.

Using melt¶

  • The melt method is common enough that we'll give it a special mention.
  • We'll often encounter pivot tables (esp. from government data), which we call wide data.
  • The methods we've introduced work better with long-form data, or tidy data.
  • To go from wide to long, melt.
No description has been provided for this image

Example usage of melt¶

In [49]:
wide_example = pd.DataFrame({
    'Year': [2001, 2002],
    'Jan': [10, 130],
    'Feb': [20, 200],
    'Mar': [30, 340]
}).set_index('Year')
wide_example
Out[49]:
Jan Feb Mar
Year
2001 10 20 30
2002 130 200 340
In [50]:
wide_example.melt(ignore_index=False)
Out[50]:
variable value
Year
2001 Jan 10
2002 Jan 130
2001 Feb 20
2002 Feb 200
2001 Mar 30
2002 Mar 340

Exploration¶

Question 🤔 (Answer at dsc80.com/q)

Code: lec05-qs

What questions do you want me to try and answer with the data? I'll start with a single pre-prepared question, and then answer student questions until we run out of time.

Example question: Can we rank restaurants by their number of violations? How about separately for each zip code?¶

And why would we want to do that? 🤔

In [ ]:

Summary, next time¶

Summary¶

  • Data cleaning is a necessary starting step in data analysis. There are four pillars of data cleaning:
    • Quality checks.
    • Missing values.
    • Transformations and timestamps.
    • Modifying structure.
  • Approach EDA with an open mind, and draw lots of visualizations.

Next time¶

Hypothesis and permutation testing. Some of this will be DSC 10 review, but we'll also push further!