from dsc80_utils import *
import plotly.io as pio
pio.renderers.default = "png"

Lecture 17 – Decision Trees and Random Forests

DSC 80, Winter 2026

Agenda 📆

• Decision trees.
• Grid search.
• Random forests.
• Modeling with text features.

Decision trees 🌲

Example: Predicting diabetes

diabetes = pd.read_csv(Path('data') / 'diabetes.csv')
display_df(diabetes, cols=9)

	Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BMI	DiabetesPedigreeFunction	Age	Outcome
0	6	148	72	35	0	33.600	0.627	50	1
1	1	85	66	29	0	26.600	0.351	31	0
2	8	183	64	0	0	23.300	0.672	32	1
...	...	...	...	...	...	...	...	...	...
765	5	121	72	23	112	26.200	0.245	30	0
766	1	126	60	0	0	30.100	0.349	47	1
767	1	93	70	31	0	30.400	0.315	23	0

768 rows × 9 columns

Exploring the dataset

First, a train-test split:

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = (
    train_test_split(diabetes[['Glucose', 'BMI']], diabetes['Outcome'], random_state=1)
)

Class 0 (orange) is "no diabetes" and class 1 (blue) is "diabetes".

fig = (
    X_train.assign(Outcome=y_train.astype(str))
            .plot(kind='scatter', x='Glucose', y='BMI', color='Outcome', 
                  color_discrete_map={'0': 'orange', '1': 'blue'},
                  title='Relationship between Glucose, BMI, and Diabetes')
)
fig
fig.show()

Building a decision tree

from sklearn.tree import DecisionTreeClassifier

dt = DecisionTreeClassifier(max_depth=2, criterion='entropy')
dt.fit(X_train, y_train)

DecisionTreeClassifier(criterion='entropy', max_depth=2)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Visualizing decision trees

Our fit decision tree is like a "flowchart", made up of a series of questions.

As before, orange is "no diabetes" and blue is "diabetes".

from sklearn.tree import plot_tree

plt.figure(figsize=(15, 5))
plot_tree(dt, feature_names=X_train.columns, class_names=['no db', 'yes db'], 
          filled=True, fontsize=15, impurity=False);

• To classify a new data point, we start at the top and answer the first question (i.e. "Glucose <= 129.5").

• If the answer is "Yes", we move to the left branch, otherwise we move to the right branch.

• We repeat this process until we end up at a leaf node, at which point we predict the most common class in that node.
  • Note that each node has a value attribute, which describes the number of training individuals of each class that fell in that node.

# Note that the left node at depth 2 has a `value` of [304, 78].
y_train[X_train.query('Glucose <= 129.5').index].value_counts()

Outcome
0    304
1     78
Name: count, dtype: int64

Evaluating classifiers

The most common evaluation metric in classification is accuracy:

$$\text{accuracy} = \frac{\text{\# data points classified correctly}}{\text{\# data points}}$$

(dt.predict(X_train) == y_train).mean()

0.765625

The score method of a classifier computes accuracy by default (just like the score method of a regressor computes $R^2$ by default). We want our classifiers to have high accuracy.

# Training accuracy – same number as above
dt.score(X_train, y_train)

0.765625

# Testing accuracy
dt.score(X_test, y_test)

0.7760416666666666

Reflection

• Decision trees are easily interpretable: it is clear how they make their predictions.

• They work with categorical data without needing to use one hot encoding.

• They also can be used in multi-class classification problems, e.g. when there are more than 2 possible outcomes.

• The decision boundary of a decision tree can be arbitrarily complicated.

• How are decision trees trained?

How are decision trees trained?

Pseudocode:

def make_tree(X, y):
    if all points in y have the same label C:
        return Leaf(C)
    f = best splitting feature # e.g. Glucose or BMI
    v = best splitting value   # e.g. 129.5
    
    X_left, y_left   = X, y where (X[f] <= v)
    X_right, y_right = X, y where (X[f] > v)
    
    left  = make_tree(X_left, y_left)
    right = make_tree(X_right, y_right)
    
    return Node(f, v, left, right)
    
make_tree(X_train, y_train)

How do we measure the quality of a split?

Our pseudocode for training a decision tree relies on finding the best way to "split" a node – that is, the best question to ask to help us narrow down which class to predict.

Intuition: Suppose the distribution within a node looks like this (colors represent classes):

🟠🟠🟠🟠🟠🟠🔵🔵🔵🔵🔵🔵🔵

Question A:

• "Yes": 🟠🟠🟠🔵🔵🔵
• "No": 🟠🟠🟠🔵🔵🔵🔵

Question B:

• "Yes": 🔵🔵🔵🔵🔵🔵
• "No": 🔵🟠🟠🟠🟠🟠🟠

Which is the "better" question to ask?

Question B, because there is "less uncertainty" in the resulting nodes. Let's try and quantify this!

Entropy

• For each class $C$ within a node, define $p_C$ as the proportion of points with that class.
  • For example, the two classes may be "yes diabetes" and "no diabetes".

• The surprise of drawing a point from the node at random and having it be class $C$ is:

$$ \log_2 \left(\frac{1}{p_C}\right) = - \log_2 p_C $$

• The entropy of a node is the expected (average) surprise over all classes:

\begin{align} \text{entropy} &= - \sum_C p_C \log_2 p_C \end{align}

• The entropy of 🟠🟠🟠🟠🟠🟠🟠🟠 is $ -1 \log_2(1) = 0 $.

• The entropy of 🟠🟠🟠🟠🔵🔵🔵🔵 is $ -0.5 \log_2(0.5) - 0.5 \log_2(0.5) = 1$.

• The entropy of 🟠🔵🟢🟡🟣 is $ - \log_2 \frac{1}{5} = \log_2(5) $
  • In general, if a node has $n$ points, all with different labels, the entropy of the node is $ \log_2(n) $.

Example entropy calculation

Suppose we have:

🟠🟠🟠🟠🟠🟠🟠🟠🟠🟠🟠🟠🔵🔵🔵🔵🔵🔵

Question A:

• "Yes": 🟠🟠🟠🟠🟠🟠🔵
• "No": 🟠🟠🟠🟠🟠🟠🔵🔵🔵🔵🔵

Question B:

• "Yes": 🟠🟠🟠🟠🟠🟠🔵🔵🔵
• "No": 🟠🟠🟠🟠🟠🟠🔵🔵🔵

We choose to ask the question that has the lowest weighted entropy, that is:

$$\text{entropy of question} = \frac{\# \text{Yes}}{\# \text{Yes} + \# \text{No}} \cdot \text{entropy(Yes)} + \frac{\# \text{No}}{\# \text{Yes} + \# \text{No}} \cdot \text{entropy(No)}$$

def entropy(node):
    props = pd.Series(list(node)).value_counts(normalize=True)
    return -sum(props * np.log2(props))

entropy("🟠🟠🟠🟠🟠🟠🔵")

0.5916727785823275

def weighted_entropy(yes_node, no_node):
    yes_entropy = entropy(yes_node)
    no_entropy = entropy(no_node)
    yes_weight = len(yes_node) / (len(yes_node) + len(no_node))
    no_weight = 1 - yes_weight
    return yes_weight * yes_entropy + (no_weight) * no_entropy

# Question A:
weighted_entropy("🟠🟠🟠🟠🟠🟠🔵", "🟠🟠🟠🟠🟠🟠🔵🔵🔵🔵🔵")

0.8375578764623786

# Question B:
weighted_entropy("🟠🟠🟠🟠🟠🟠🔵🔵🔵", "🟠🟠🟠🟠🟠🟠🔵🔵🔵")

0.9182958340544896

Question A has the lower weighted entropy, so we'll use it.

Understanding entropy

plt.figure(figsize=(10, 5))
plot_tree(dt, feature_names=X_train.columns, class_names=['no db', 'yes db'], 
          filled=True, fontsize=15, impurity=True);

We can recreate the entropy calculations in this tree.

# The leftmost node at the middle level has an entropy of 0.73,
# both displayed in the tree and verified here!
entropy([0] * 304 + [1] * 78)

0.7302263747422792

Note: The default DecisionTreeClassifier uncertaintly metric isn't entropy, it is Gini impurity. Our tree shows entropy because we set criterion='entropy' when defining dt.

Question 🤔

(From Fa23 Final)

Suppose we fit decision trees of varying depths to predict 'y' using 'x1' and 'x2'. The entire training set is shown in the table below.

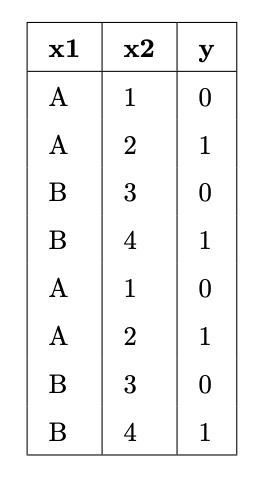
What is:

1. The entropy of a node containing all the training points.
2. The lowest possible entropy of a node in a fitted tree with depth 1 (two leaf nodes).
3. The lowest possible entropy of a node in a fitted tree with depth 2 (four leaf nodes).

Tree depth

Decision trees are trained by recursively picking the best split until:

• all "leaf nodes" contain only training examples from a single class,
• it is impossible to split leaf nodes any further, or
• some other stopping criteria is reached.

By default, there are no additional stopping criteria, so decision trees tend to be very deep when unrestricted.

dt_no_max = DecisionTreeClassifier()
dt_no_max.fit(X_train, y_train)

DecisionTreeClassifier()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

A decision tree fit on our training data is so deep that tree.plot_tree errors when trying to plot it.

dt_no_max.tree_.max_depth

20

At first, this tree seems "better" than our initial tree of depth 2, since its training accuracy is much much higher:

dt_no_max.score(X_train, y_train)

0.9913194444444444

# Depth 2 tree.
dt.score(X_train, y_train)

0.765625

But recall, we truly care about test set performance, and this decision tree has worse accuracy on the test set than our depth 2 tree.

dt_no_max.score(X_test, y_test)

0.7239583333333334

# Depth 2 tree.
dt.score(X_test, y_test)

0.7760416666666666

Decision trees and overfitting

• Decision trees have a tendency to overfit. Why is that?

• Unlike linear classification techniques (like logistic regression or SVMs), decision trees are non-linear.
  • They are also "non-parametric", which means we don't need to make any assumptions about the underlying distribution of the data in nature.

• While being trained, decision trees ask enough questions to effectively memorize the correct response values in the training set. However, the relationships they learn are often overfit to the noise in the training set, and don't generalize well.

fig
fig.show()

• A decision tree whose depth is not restricted will achieve 100% accuracy on any training set, as long as there are no "overlapping values" in the training set.
  • Two values overlap when they have the same features $x$ but different response values $y$ (e.g. if two patients have the same glucose levels and BMI, but one has diabetes and one doesn't).

• One solution to overfitting: Make the decision tree "less complex" by limiting the maximum depth.

trees = {}
for d in [2, 4, 8]:
    trees[d] = DecisionTreeClassifier(max_depth=d, random_state=1)
    trees[d].fit(X_train, y_train)
    
    plt.figure(figsize=(10, 5), dpi=100)
    plot_tree(trees[d], feature_names=X_train.columns, class_names=['no db', 'yes db'], 
               filled=True, rounded=True, impurity=False)
    
    plt.show()

As tree depth increases, complexity increases, and our trees are more prone to overfitting. This means model bias decreases, but model variance increases.

Question: What is the "right" maximum depth to choose?

Hyperparameters for decision trees

• max_depth is a hyperparameter for DecisionTreeClassifier.

• There are many more hyperparameters we can tweak; look at the documentation for examples.
  • min_samples_split: The minimum number of samples required to split an internal node.
  • criterion: The function to measure the quality of a split ('gini' or 'entropy').

• To ensure that our model generalizes well to unseen data, we need an efficient technique for trying different combinations of hyperparameters!

Grid search 🔎

Grid search

GridSearchCV takes in:

• an un-fit instance of an estimator, and
• a dictionary of hyperparameter values to try,

and performs $k$-fold cross-validation to find the combination of hyperparameters with the best average validation performance.

from sklearn.model_selection import GridSearchCV

The following dictionary contains the values we're considering for each hyperparameter. (We're using GridSearchCV with 3 hyperparameters, but we could use it with even just a single hyperparameter.)

hyperparameters = {
    'max_depth': [2, 3, 4, 5, 7, 10, 15, 20, 25, 50], 
    'min_samples_split': [2, 5, 10, 20, 50, 100, 200],
    'criterion': ['gini', 'entropy']
}

Note that there are 140 combinations of hyperparameters we need to try. We need to find the best combination of hyperparameters, not the best value for each hyperparameter individually.

len(hyperparameters['max_depth']) * \
len(hyperparameters['min_samples_split']) * \
len(hyperparameters['criterion'])

140

GridSearchCV needs to be instantiated and fit.

searcher = GridSearchCV(DecisionTreeClassifier(), hyperparameters, cv=5)

%%time
searcher.fit(X_train, y_train)

CPU times: user 1.29 s, sys: 10.5 ms, total: 1.3 s
Wall time: 1.32 s

/Users/msgol/ENTER/envs/dsc80/lib/python3.12/site-packages/numpy/ma/core.py:2820: RuntimeWarning:

invalid value encountered in cast

GridSearchCV(cv=5, estimator=DecisionTreeClassifier(),
             param_grid={'criterion': ['gini', 'entropy'],
                         'max_depth': [2, 3, 4, 5, 7, 10, 15, 20, 25, 50],
                         'min_samples_split': [2, 5, 10, 20, 50, 100, 200]})

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

After being fit, the best_params_ attribute provides us with the best combination of hyperparameters to use.

searcher.best_params_

{'criterion': 'gini', 'max_depth': 4, 'min_samples_split': 50}

All of the intermediate results – validation accuracies for each fold, mean validation accuaries, etc. – are stored in the cv_results_ attribute:

searcher.cv_results_['mean_test_score'] # Array of length 140.

array([0.73, 0.73, 0.73, ..., 0.75, 0.74, 0.72])

# Rows correspond to folds, columns correspond to hyperparameter combinations.
pd.DataFrame(np.vstack([searcher.cv_results_[f'split{i}_test_score'] for i in range(5)]))

	0	1	2	3	...	136	137	138	139
0	0.707	0.707	0.707	0.707	...	0.672	0.698	0.707	0.733
1	0.774	0.774	0.774	0.774	...	0.817	0.826	0.774	0.757
2	0.739	0.739	0.739	0.739	...	0.678	0.722	0.739	0.730
3	0.704	0.704	0.704	0.704	...	0.765	0.791	0.757	0.696
4	0.722	0.722	0.722	0.722	...	0.704	0.713	0.722	0.704

5 rows × 140 columns

Note that the above DataFrame tells us that 5 * 140 = 700 models were trained in total!

Now that we've found the best combination of hyperparameters, we should fit a decision tree instance using those hyperparameters on our entire training set.

searcher.best_params_

{'criterion': 'gini', 'max_depth': 4, 'min_samples_split': 50}

final_tree = DecisionTreeClassifier(**searcher.best_params_)
final_tree

DecisionTreeClassifier(max_depth=4, min_samples_split=50)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

final_tree.fit(X_train, y_train)

DecisionTreeClassifier(max_depth=4, min_samples_split=50)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# Training accuracy.
final_tree.score(X_train, y_train)

0.7881944444444444

# Testing accuracy.
# A bit lower than the `dt` tree we fit above!
final_tree.score(X_test, y_test)

0.765625

Remember, searcher itself is a model object (we had to fit it). After performing $k$-fold cross-validation, behind the scenes, searcher is automatically trained on the entire training set using the optimal combination of hyperparameters.

In other words, searcher makes the same predictions that final_tree does!

searcher.score(X_train, y_train)

0.7881944444444444

searcher.score(X_test, y_test)

0.765625

Choosing possible hyperparameter values

• A full grid search can take a long time.

  • In our previous example, we tried 140 combinations of hyperparameters.
  • Since we performed 5-fold cross-validation, we trained 700 decision trees under the hood.

• Question: How do we pick the possible hyperparameter values to try?

• Answer: Trial and error.

  • If the "best" choice of a hyperparameter was at an extreme, try increasing the range.
  • For instance, if you try max_depths from 32 to 128, and 32 was the best, try including max_depths under 32.

Key takeaways

• Decision trees are trained by finding the best questions to ask using the features in the training data. A good question is one that isolates classes as much as possible.
• Decision trees have a tendency to overfit to training data. One way to mitigate this is by restricting the maximum depth of the tree.
• To efficiently find hyperparameters through cross-validation, use GridSearchCV.
  • Specify which values to try for each hyperparameter, and GridSearchCV will try all combinations of hyperparameters and return the combination with the best average validation performance.
  • GridSearchCV is not the only solution – see RandomizedSearchCV if you're curious.

Decision tree pros and cons

✅ Pros:

• Relatively fast to train and make predictions.
  • Making predictions: $O(\text{tree depth})$, which is usually $O(\log n)$.
• Easily interpretable.
• Robust to irrelevant features – why?
• Works with categorical and numerical data. Doesn't require much preprocessing (feature engineering).

❌ Cons:

• High variance: with no limitations (e.g. max_depth), will almost always overfit!
• Creates biased predictions if classes are unbalanced.
• Not the best at prediction in general (sensitive to outliers and noise in the training data, not good at extrapolating outside of the training data).

sklearn's documentation provides a good overview of the pros and cons of decision trees.

Random Forests

Another idea:

Train a bunch of decision trees, then have them vote on a prediction!

• Problem: If you use the same training data, you will always get the same tree.
• Solution: Introduce randomness into training procedure to get different trees.

Idea 1: Bootstrap the training data

• We can bootstrap the training data $T$ times, then train one tree on each resample.
• Also known as bagging (Bootstrap AGgregating). In general, combining different predictors together is a useful technique called ensemble learning.
• For decision trees though, this doesn't make the trees different enough from each other (e.g. if you have one really strong predictor, it will always be the first split).

Idea 2: At each split, use a subset of features

• At each split, take a random subset of $ m $ features instead of choosing from all $ d $ of them.

• Rule of thumb: $ m \approx \sqrt d $ seems to work well.

• Key idea: For ensemble learning, you want the individual predictors to have low bias, high variance, and be uncorrelated with each other. That way, when you average them together, you have low bias AND low variance.

• Random forest algorithm: Fit $ T $ trees by using bagging and a random subset of features at each split. Predict by taking a vote from the $ T $ trees.

Question 🤔

How will increasing $ m $ affect the bias / variance of each decision tree?

Example

# Let's use more features for prediction
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = (
    train_test_split(diabetes.drop(columns=['Outcome']), diabetes['Outcome'], random_state=1)
)

from sklearn.ensemble import RandomForestClassifier

rf = RandomForestClassifier()
rf.fit(X_train, y_train)
rf.score(X_train, y_train)

1.0

rf.score(X_test, y_test)

0.7864583333333334

This is better than our best single decision tree from earlier.

Example: Modeling using text features

Example: Fake news

We have a dataset (source) containing news articles and labels for whether the article was deemed "fake" or "real".

news = pd.read_csv('data/fake_news_training.csv')
news

	baseurl	content	label
0	twitter.com	\njavascript is not available.\n\nwe’ve detect...	real
1	whitehouse.gov	remarks by the president at campaign event -- ...	real
2	web.archive.org	the committee on energy and commerce\nbarton: ...	real
...	...	...	...
658	politico.com	full text: jeff flake on trump speech transcri...	fake
659	pol.moveon.org	moveon.org political action: 10 things to know...	real
660	uspostman.com	uspostman.com is for sale\nyes, you can transf...	fake

661 rows × 3 columns

Goal: Use an article's content to predict its label.

news['label'].value_counts(normalize=True)

label
real   0.549
fake   0.451
Name: proportion, dtype: float64

Question: What is the worst possible accuracy we should expect from a classifier, given the above distribution?

Aside: CountVectorizer

Entries in the 'content' column are not currently quantitative! We can use the bag of words encoding to create quantitative features out of each 'content'.

Instead of performing a bag of words encoding manually as we did before, we can rely on sklearn's CountVectorizer. (There is also a TfidfVectorizer.)

from sklearn.feature_extraction.text import CountVectorizer

nursery_rhymes = ['Jack be nimble, Jack be quick, Jack jump over the candlestick.', 
                  'Jack and Jill went up the hill to fetch a pail of water.',
                  'Little Jack Horner sat in the corner eating a Christmas pie.']

count_vec = CountVectorizer()
count_vec.fit(nursery_rhymes)

CountVectorizer()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

count_vec learned a vocabulary from the corpus we fit it on.

count_vec.vocabulary_

{'jack': 10,
 'be': 1,
 'nimble': 14,
 'quick': 19,
 'jump': 12,
 'over': 16,
 'the': 21,
 'candlestick': 2,
 'and': 0,
 'jill': 11,
 'went': 25,
 'up': 23,
 'hill': 7,
 'to': 22,
 'fetch': 6,
 'pail': 17,
 'of': 15,
 'water': 24,
 'little': 13,
 'horner': 8,
 'sat': 20,
 'in': 9,
 'corner': 4,
 'eating': 5,
 'christmas': 3,
 'pie': 18}

count_vec.transform(nursery_rhymes).toarray()

array([[0, 2, 1, ..., 0, 0, 0],
       [1, 0, 0, ..., 1, 1, 1],
       [0, 0, 0, ..., 0, 0, 0]])

Note that count_vec.vocabulary_ is a dictionary that maps each word to the associated column in the array above. For example, the first column corresponds to 'and'.

nursery_rhymes

['Jack be nimble, Jack be quick, Jack jump over the candlestick.',
 'Jack and Jill went up the hill to fetch a pail of water.',
 'Little Jack Horner sat in the corner eating a Christmas pie.']

pd.DataFrame(count_vec.transform(nursery_rhymes).toarray(),
             columns=pd.Series(count_vec.vocabulary_).sort_values().index)

	and	be	candlestick	christmas	...	to	up	water	went
0	0	2	1	0	...	0	0	0	0
1	1	0	0	0	...	1	1	1	1
2	0	0	0	1	...	0	0	0	0

3 rows × 26 columns

Creating an initial Pipeline

Let's build a Pipeline that takes in summaries and overall ratings and:

• Uses CountVectorizer to quantitatively encode summaries.

• Fits a RandomForestClassifier to the data.

But first, a train-test split (like always).

from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.ensemble import RandomForestClassifier

X = news['content']
y = news['label']
X_train, X_test, y_train, y_test = train_test_split(X, y)

To start, we'll create a random forest with 100 trees (n_estimators) each of which has a maximum depth of 3 (max_depth).

pl = Pipeline([
    ('bag-of-words', CountVectorizer()), 
    ('forest', RandomForestClassifier(
        max_depth=3,
        n_estimators=100, # Uses 100 separate decision trees!
        random_state=42,
    )) 
])

pl.fit(X_train, y_train)

Pipeline(steps=[('bag-of-words', CountVectorizer()),
                ('forest',
                 RandomForestClassifier(max_depth=3, random_state=42))])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# Training accuracy.
pl.score(X_train, y_train)

0.7919191919191919

# Testing accuracy.
pl.score(X_test, y_test)

0.7409638554216867

The accuracy of our random forest is just under 70%, on the test set. How much better does it do compared to a classifier that predicts "real" every time?

y_train.value_counts(normalize=True)

label
real   0.578
fake   0.422
Name: proportion, dtype: float64

# Distribution of predicted ys in the training set:

# stops scientific notation for pandas
pd.set_option('display.float_format', '{:.3f}'.format)
pd.Series(pl.predict(X_train)).value_counts(normalize=True)

fake   0.549
real   0.451
Name: proportion, dtype: float64

Choosing tree depth via GridSearchCV

We arbitrarily chose max_depth=3 before, but it seems like that isn't working well. Let's perform a grid search to find the max_depth with the best generalization performance.

# Note that we've used the key forest__max_depth, not max_depth
# because max_depth is a hyperparameter of the step we called "forest".
# It is not a hyperparameter of the pipeline, pl.

hyperparameters = {
    'forest__max_depth': np.arange(2, 200, 20)
}

Note that while pl has already been fit, we can still give it to GridSearchCV, which will repeatedly re-fit it during cross-validation.

%%time

# Takes a few seconds to run – how many trees are being trained?
from sklearn.model_selection import GridSearchCV
grids = GridSearchCV(
    pl,
    n_jobs=-1, # Use multiple processors to parallelize
    param_grid=hyperparameters,
    return_train_score=True
)
grids.fit(X_train, y_train)

CPU times: user 1.56 s, sys: 275 ms, total: 1.84 s
Wall time: 8.91 s

GridSearchCV(estimator=Pipeline(steps=[('bag-of-words', CountVectorizer()),
                                       ('forest',
                                        RandomForestClassifier(max_depth=3,
                                                               random_state=42))]),
             n_jobs=-1,
             param_grid={'forest__max_depth': array([  2,  22,  42,  62,  82, 102, 122, 142, 162, 182])},
             return_train_score=True)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

grids.best_params_

{'forest__max_depth': 82}

Recall, fit GridSearchCV objects are estimators on their own as well. This means we can compute the training and testing accuracies of the "best" random forest directly:

# Training accuracy.
grids.score(X_train, y_train)

0.9939393939393939

# Testing accuracy.
grids.score(X_test, y_test)

0.8192771084337349

# Compare to our original model with max_depth = 3.
pl.score(X_test, y_test)

0.7409638554216867

~15% better test set error!

Training and validation accuracy vs. depth

Below, we plot how training and validation accuracy varied with tree depth. Note that the $y$-axis here is accuracy, and that larger accuracies are better (unlike with RMSE, where smaller was better).

index = grids.param_grid['forest__max_depth']
train = grids.cv_results_['mean_train_score']
valid = grids.cv_results_['mean_test_score']

pd.DataFrame({'train': train, 'valid': valid}, index=index).plot().update_layout(
    xaxis_title='max_depth', yaxis_title='Accuracy'
)

Question 🤔

(From Fa23 Final)

Suppose we write the following code:

hyperparameters = {
    'n_estimators': [10, 100, 1000], # number of trees per forest
    'max_depth': [None, 100, 10]     # max depth of each tree
}
grids = GridSearchCV(
    RandomForestClassifier(), param_grid=hyperparameters,
    cv=3, # 3-fold cross-validation
)
grids.fit(X_train, y_train)

Answer the following questions with a single number.

1. How many random forests are fit in total?
2. How many decision trees are fit in total?
3. How many times in total is the first point in X_train used to train a decision tree?

Classifier Evaluation

Accuracy isn't everything!

$$ \text{accuracy} = \frac{\text{\# data points classified correctly}}{\text{\# data points}} $$

• Accuracy is defined as the proportion of predictions that are correct.

• It weighs all correct predictions the same, and weighs all incorrect predictions the same.

• But some incorrect predictions may be worse than others!

  • Example: diagnosing a disease when a person doesn't have it vs. not diagnosing a disease when a person does have it.

The Boy Who Cried Wolf 👦😭🐺

(source)

The tale concerns a shepherd boy who repeatedly tricks villagers into believing a wolf is attacking his flock. When a real wolf appears and the boy cries for help, the villagers dismiss it as another false alarm, allowing the wolf to devour the sheep.

The wolf classifier

• Predictor: Shepherd boy.
• Positive prediction: "There is a wolf."
• Negative prediction: "There is no wolf."

Some questions to think about:

• What is an example of an incorrect, positive prediction?

• Was there a correct, negative prediction?

• There are four possibilities. What are the consequences of each?
  • (predict yes, predict no) x (actually yes, actually no).

Outcomes in binary classification

When performing binary classification, there are four possible outcomes.

Outcome of Prediction	Definition	True Class
True positive (TP) ✅	The predictor correctly predicts the positive class.	P
False negative (FN) ❌	The predictor incorrectly predicts the negative class.	P
True negative (TN) ✅	The predictor correctly predicts the negative class.	N
False positive (FP) ❌	The predictor incorrectly predicts the positive class.	N

⬇️

	Predicted Negative	Predicted Positive
Actually Negative	TN ✅	FP ❌
Actually Positive	FN ❌	TP ✅

The confusion matrix above summarizes the four possibilities.

Note that in the four acronyms – TP, FN, TN, FP – the first letter is whether the prediction is correct, and the second letter is what the prediction is.

Example: Measles outbreak 🔴

• Measles is a highly contagious disease that can cause severe illness. The number of measles cases in the US has surged in recent months.

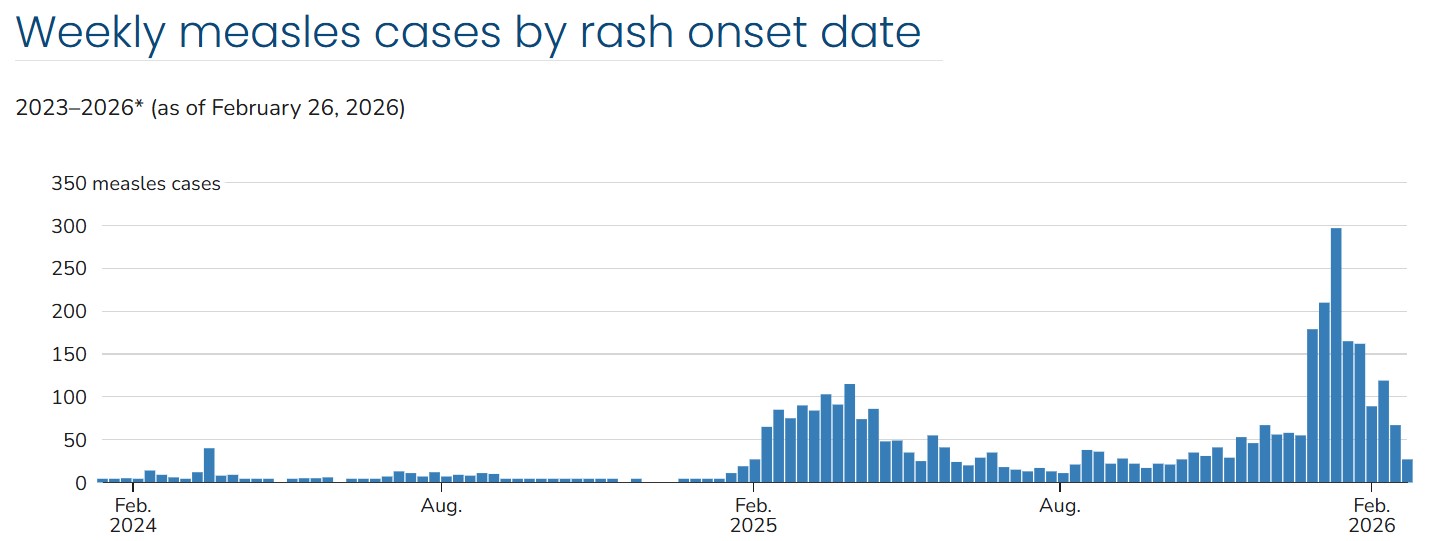
• Tests exist to identify active measles infections. Tests can come back
  • positive, indicating that the individual has measles, or
  • negative, indicating that the individual does not have measles.

Question 🤔

What is a TP in this scenario? FP? TN? FN?

Accuracy of measles tests

The results of 100 measles tests are given below.

	Predicted Negative	Predicted Positive
Actually Negative	TN = 90 ✅	FP = 1 ❌
Actually Positive	FN = 8 ❌	TP = 1 ✅

🤔 Question: What is the accuracy of the test?

🙋 Answer: $$\text{accuracy} = \frac{TP + TN}{TP + FP + FN + TN} = \frac{1 + 90}{100} = 0.91$$

• Followup: At first, the test seems good. But, suppose we build a classifier that predicts that nobody has measles. What would its accuracy be?

• Answer to followup: Also 0.91! There is severe class imbalance in the dataset, meaning that most of the data points are in the same class (no measles). Accuracy doesn't tell the full story.

Recall

	Predicted Negative	Predicted Positive
Actually Negative	TN = 90 ✅	FP = 1 ❌
Actually Positive	FN = 8 ❌	TP = 1 ✅

🤔 Question: What proportion of individuals who actually have measles did the test identify?

🙋 Answer: $\frac{1}{1 + 8} = \frac{1}{9} \approx 0.11$

More generally, the recall of a binary classifier is the proportion of actually positive instances that are correctly classified. We'd like this number to be as close to 1 (100%) as possible.

$$\text{recall} = \frac{TP}{\text{\# actually positive}} = \frac{TP}{TP + FN}$$

To compute recall, look at the bottom (positive) row of the above confusion matrix.

Recall isn't everything, either!

$$\text{recall} = \frac{TP}{TP + FN}$$

🤔 Question: Can you design a "measles test" with perfect recall?

🙋 Answer: Yes – just predict that everyone has measles!

	Predicted Negative	Predicted Positive
Actually Negative	TN = 0 ✅	FP = 91 ❌
Actually Positive	FN = 0 ❌	TP = 9 ✅

everyone-has-measles classifier

$$\text{recall} = \frac{TP}{TP + FN} = \frac{9}{9 + 0} = 1$$

Like accuracy, recall on its own is not a perfect metric. Even though the classifier we just created has perfect recall, it has 91 false positives!

Precision

	Predicted Negative	Predicted Positive
Actually Negative	TN = 0 ✅	FP = 91 ❌
Actually Positive	FN = 0 ❌	TP = 9 ✅

everyone-has-measles classifier

The precision of a binary classifier is the proportion of predicted positive instances that are correctly classified. We'd like this number to be as close to 1 (100%) as possible.

$$\text{precision} = \frac{TP}{\text{\# predicted positive}} = \frac{TP}{TP + FP}$$

To compute precision, look at the right (positive) column of the above confusion matrix.

• Tip: A good way to remember the difference between precision and recall is that in the denominator for 🅿️recision, both terms have 🅿️ in them (TP and FP).

• Note that the "everyone-has-measles" classifier has perfect recall, but a precision of $\frac{9}{9 + 91} = 0.09$, which is quite low.

• 🚨 Key idea: There is a "tradeoff" between precision and recall. Ideally, you want both to be high. For a particular prediction task, one may be important than the other.

Precision and recall

$$\text{precision} = \frac{TP}{TP + FP} \: \: \: \: \: \: \: \: \text{recall} = \frac{TP}{TP + FN}$$

Question

• When might high precision be more important than high recall?

• When might high recall be more important than high precision?

Precision and recall

(source)

Question 🤔

Consider the confusion matrix shown below.

	Predicted Negative	Predicted Positive
Actually Negative	TN = 22 ✅	FP = 2 ❌
Actually Positive	FN = 23 ❌	TP = 18 ✅

What is the accuracy of the above classifier? The precision? The recall?

Summary, next time

Summary

• Decision trees, while interpretable, are prone to having high variance. There are several ways to control the variance of a decision tree:
  • Limit max_depth or increase min_samples_split.
  • Create a random forest, which is an ensemble of multiple decision trees, each fit to a different random resample of the training data, using a random sample of features.
• In order to tune model hyperparameters – that is, to find the hyperparameters that likely maximize performance on unseen data – use GridSearchCV.
• Accuracy alone is not always a meaningful representation of a classifier's quality, particularly when the classes are imbalanced.
  • Precision and recall are classifier evaluation metrics that consider the types of errors being made.
  • There is a "tradeoff" between precision and recall. One may be more important than the other, depending on the task.

Next time

We'll continue our discussion of evaluating classifiers and talk about model fairness, which is part of your Final Project.